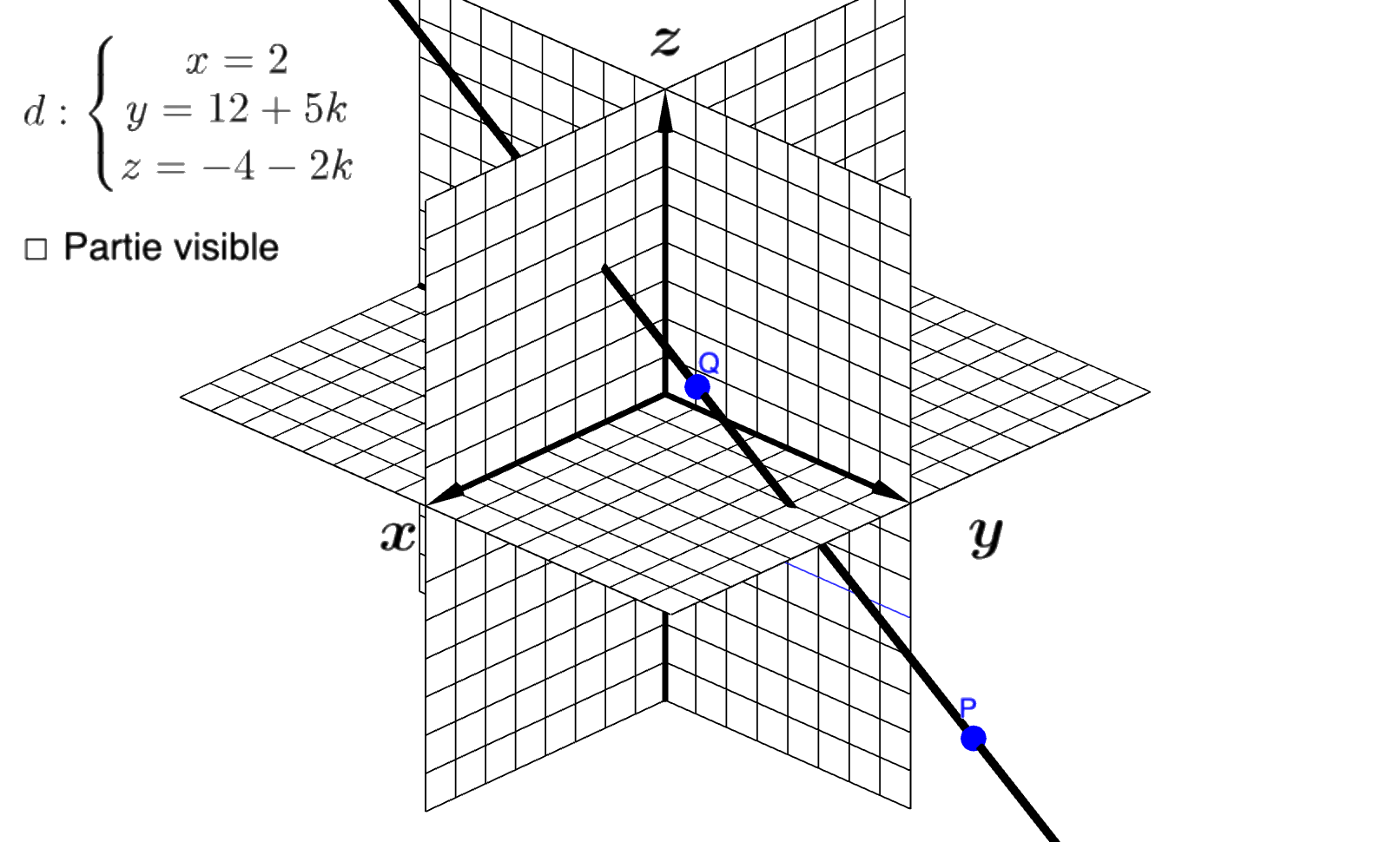
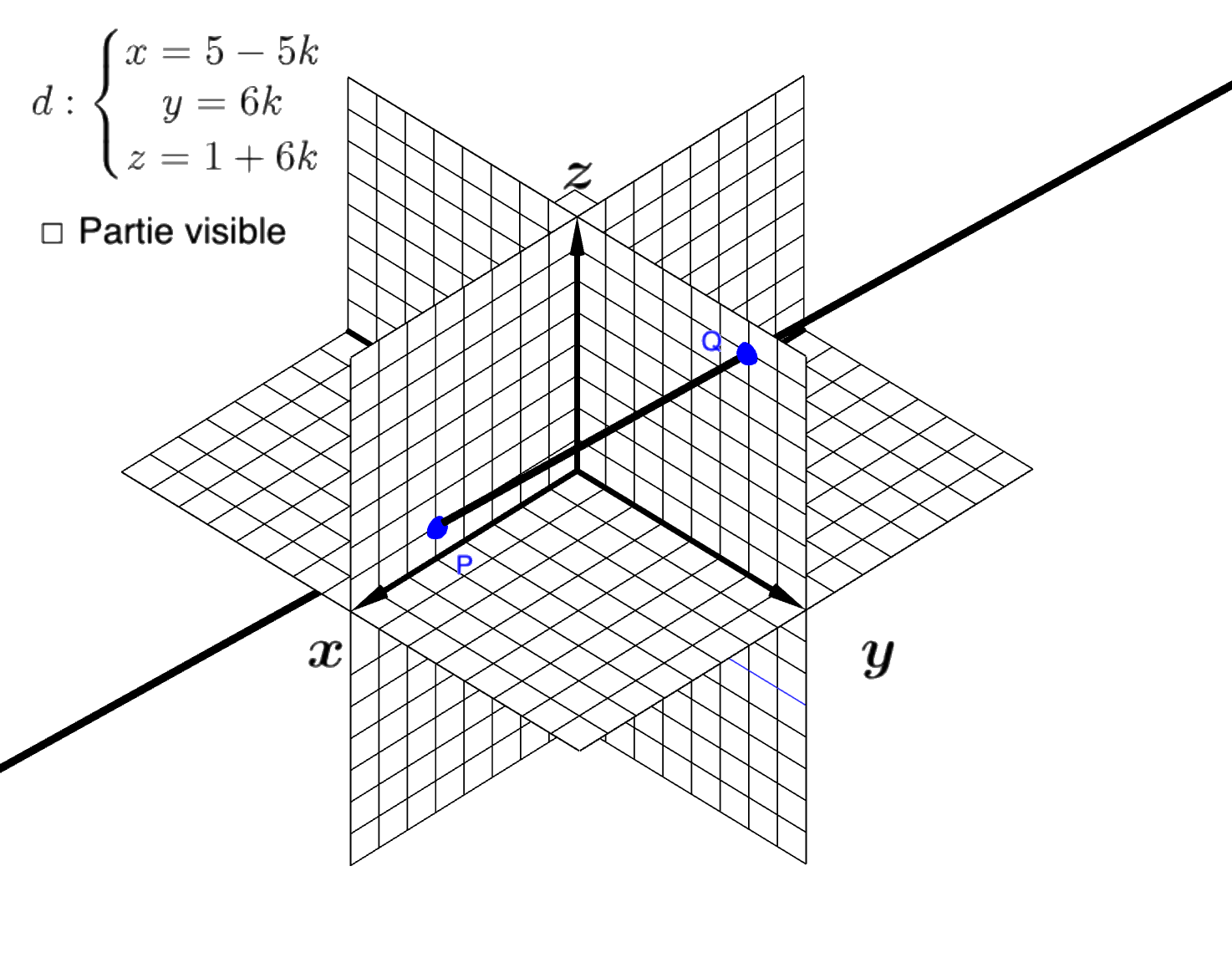
La représentation vectorielle ou paramétrique d’une droite dans l’espace est de type :
On peut aussi l’écrire sous une autre forme :
Dans cette représentation x0, y0 et z0 sont les coordonnées d’un point appartenant à la droite et xv, yv et zv sont les composantes d’un vecteur parallèle à la droite (vecteur directeur). Il existe une infinité de points sur une droite et une infinité de vecteurs parallèles à une droite. Ainsi, selon le point et le vecteur choisis, il existe ainsi une infinité de représentations vectorielles d’une même droite.
Cliquez sur une image pour voir un exemple :
Pour savoir comment déterminer la partie visible d’une droite, cliquez ici.