Un corps sur un plan incliné peut être immobile ou en mouvement. Selon les situations le corps peut descendre ou monter le plan. Ce mouvement peut être à vitesse constante (MRU) ou avec une accélération constante (MRUA). Su un plan incliné on dispose donc de toutes les lois et règles concernant ces mouvements dont voici un rappel (pour plus de détails voir le cours sur les mouvements rectilignes) :
| MRU | ||
| Vitesse moyenne | La vitesse est constante donc la vitesse moyenne est vitesse instantanée sont identiques. | |
| Vitesse instantanée | ||
| Distance | ||
| Durée | ||
| Accélération | La vitesse est constante donc l’accélération est nulle. | |
| Forces | Selon la loi fondamentale la résultante de toutes les forces . Si l’accélération est nulle la force résultante est aussi nulle. | |
| Poids | Lors d’un mouvement sur un plan horizontal le poids est une force perpendiculaire au mouvement et n’y joue donc aucun rôle. | |
| MRUA | ||
| Vitesse moyenne | ||
| Vitesse instantanée | ||
| Distance | ||
| Durée | ||
| Accélération | Accélération peut être positive ou négative (décélération) | |
| Forces | Selon la loi fondamentale la résultante de toutes les forces. | |
| Poids | Lors d’un mouvement sur un plan horizontal le poids est une force perpendiculaire au mouvement et n’y joue donc aucun rôle. | |
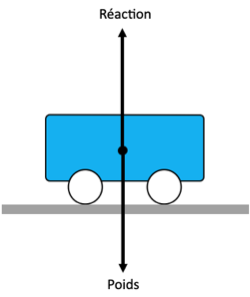 Comme vous pouvez le lire dans le rappel ci-dessous le poids ne joue aucun rôle dans un mouvement sur un plan horizontal. Pour vous en convaincre imaginez un chariot posé sur une surface horizontale. Ce chariot a un poids qui est une force verticale dirigée vers le centre de la Terre. Cette force plaque le chariot au sol mais ne peut le mettre en mouvement.
Comme vous pouvez le lire dans le rappel ci-dessous le poids ne joue aucun rôle dans un mouvement sur un plan horizontal. Pour vous en convaincre imaginez un chariot posé sur une surface horizontale. Ce chariot a un poids qui est une force verticale dirigée vers le centre de la Terre. Cette force plaque le chariot au sol mais ne peut le mettre en mouvement.
Ne confondez pas le poids qui est une force (unité : Newton) avec la masse (unité : kg) qui représente la quantité de matière constituant le chariot. Selon la loi fondamentale l’accélération est inversement proportionnelle à la masse ().
Le poids sur un plan incliné
 Sur un plan incliné la situation est différente. Le poids n’est pas perpendiculaire au déplacement et participe ainsi au mouvement. On peut parfaitement imaginer la situation où on pose un chariot sur un plan incliné : le chariot se mettra en mouvement et descendra la pente.
Sur un plan incliné la situation est différente. Le poids n’est pas perpendiculaire au déplacement et participe ainsi au mouvement. On peut parfaitement imaginer la situation où on pose un chariot sur un plan incliné : le chariot se mettra en mouvement et descendra la pente.
Sur un plan inclinée le poids a deux effets : d’une part il tire le corps vers le bas de la pente et d’autre part il plaque le corps sur le plan incliné. Remarquez que le poids est, comme sur un plan horizontal, une force verticale dirigée vers le centre de la Terre. Par contre la réaction ou la force de soutien générée par le plan n’est pas verticale comme sur un plan horizontale mais perpendiculaire au plan.
Décomposition du poids sur un plan incliné
 Pour pouvoir étudier l’effet du poids sur le mouvement on doit donc distinguer ces deux effets en le décomposant le poids (P) en deux composantes : une perpendiculaire (Fn) et une autre parallèle au déplacement (Fp) :
Pour pouvoir étudier l’effet du poids sur le mouvement on doit donc distinguer ces deux effets en le décomposant le poids (P) en deux composantes : une perpendiculaire (Fn) et une autre parallèle au déplacement (Fp) :
La composante Fn perpendiculaire (ou normale) au plan plaque le corps au sol. La réaction ou la force de soutient généré est directement opposée à cette composante : elle est de même direction mais de sens opposée à Fn. La composante Fp parallèle au mouvement tire le corps vers le bas de la pente. C’est elle qui participe à l’accélération et modifie la vitesse du corps. En absence d’autres forces notre chariot descend la pente avec une vitesse de plus en plus grande. On peut déterminer son accélération en fonction de Fp :
Ici on a supposé que le chariot était initialement immobile et ne subissait pas d’autres forces comme une force motrice ou des frottements.
Mais on peut imaginer des situations où d’autres forces agissent sur le corps : les forces frottement, une force motrice etc. Pour appliquer correctement la loi fondamentale il faut encore savoir le sens du mouvement : vers le haut ou vers le bas. Voici quelques exemples :
| Le chariot descend en roue libre sans subir des frottements : | Le chariot descend en roue libre (sans force motrice) et subit des frottements : | Le chariot monte en roue libre avec une vitesse initiale et subit des frottements : |
 |
 |
 |
| Le chariot est tiré vers le haut avec une force motrice. Il subit aussi des frottements : | Le chariot descend avec une force motrice. Il subit aussi des forces de frottement : | Le chariot descend tout en étant retenu par un câble (Tc). Il subit aussi des frottements : |
 |
 |
 |
Déterminer les composantes du poids
Sur un plan incliné le poids d’un corps (P) et ses deux composantes constituent un triangle rectangle dont la longueur de l’hypoténuse est égale à la norme du poids et les deux cathètes sont les deux composantes Fn et Fp. Notez que l’angle entre le plan incliné et l’horizon est la même que celui en face de Fp (voir schéma) :

poids est le produit de la masse par l’accélération de la gravitation : .
L’application des règles de trigonométrie nous permet de déterminer les deux composantes en fonction du poids :
et
Ainsi on connaissant la masse du corps et l’angle que fait le plan incliné avec l’horizon on peut déterminer ces deux composantes :

Pour pouvoir étudier les effets du poids sur un plan incliné il faut le considérer comme la résultante de deux composante:
- La composante perpendiculaire ou normale au plan incliné (Fn) plaque le mobile au sol. Elle engendre la force de soutient exercée par le plan sur le mobile.
- La composante parallèle au plan incliné (Fp) tire le mobile vers le bas de la pente.
Ce simulateur vous permet de voir comment les deux composantes (Fn et Fp) du poids (P) varient en fonction de la masse (m) et de l’inclinaison du plan (angle α) :
Ici on simule un mobile qui monte sur un plan incliné. Il est soumis en plus de son poids (P) à une force motrice (Fm) et des forces de frottement (Ff).
Faites varier les divers paramètres et observez comment l’accélération change en fonction de ces paramètres.
