Objectifs
- Savoir calculer les coordonnées d’un point se trouvant à 1/3 d’un segment de droite donné
- Savoir adapter cette procédure pour calculer les coordonnées d’un point se trouvant à a/b d’un segment de droite donné
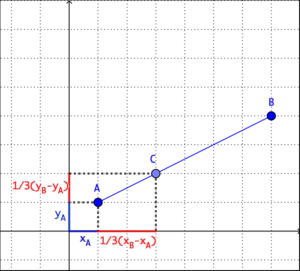
Pour calculer l’abscisse du point C qui se trouve à 1/3 de AB on utilise la formule suivante: 
. Vous n’avez pas à apprendre par coeur cette formule. Observez le schéma:
L’abscisse du point C est égale à la somme de l’abscisse du point A (xA) et de 1/3 de la distance entre les abscisses du point A et B (xB–xA). Le même raisonnement permet de calculer l’ordonnée du point C: 
.
On peut très simplement adapter cette procédure pour calculer des coordonnées de points se trouvant à d’autres endroits sur un segment. Il suffit de remplacer 1/3 par la proportion voulue. Par exemple pour trouver les coordonnées d’un point qui se trouve à 5/7 du segment AB il suffit de remplacer dans le calcul 1/3 par 5/7.
Instructions
Déplacez les points A et B. Relevez leurs coordonnées de ces points et calculez les coordonnées du point M qui se trouve à 1/3 du segment AB. Cliquez sur « Montrer les calculs » pour voir le calcul détaillé. Recommencez!